21 min to read
BFS, 너비 우선 탐색
기초 알고리즘인 BFS 를 알아보자

What is BFS?
Breadth First Search, BFS 너비 우선 탐색
대표적인 탐색 algorithm 으로 트리, 그래프 등을 탐색하는 방법 중 하나이다. 너비를 우선적으로 탐색하는 것은 특정 노드를 기준으로 인접한 주변 노드를 우선적으로 탐색한다는 뜻이다. 닿아있는 곳, 인접한 등 특정 조건으로 주변을 탐색한다. 아래의 그림을 보면 DFS 와 BFS 의 탐색 순서가 다른 것을 알 수 있다.
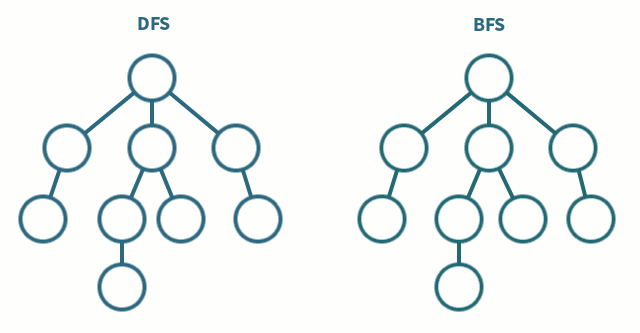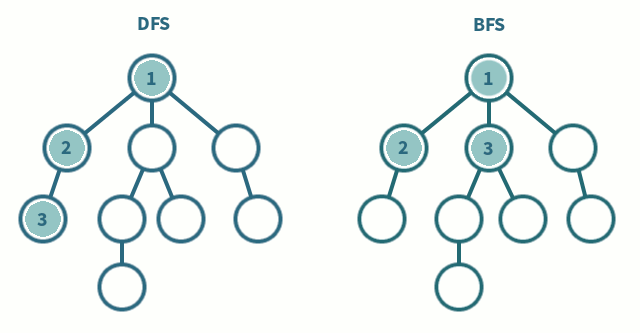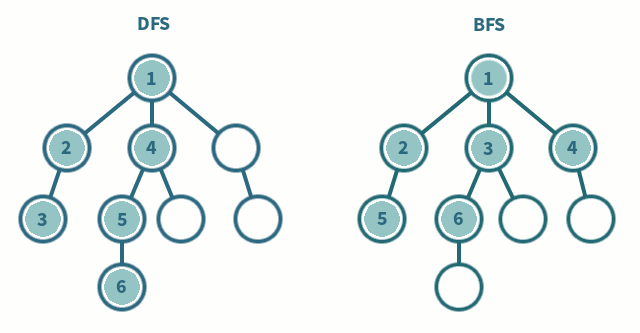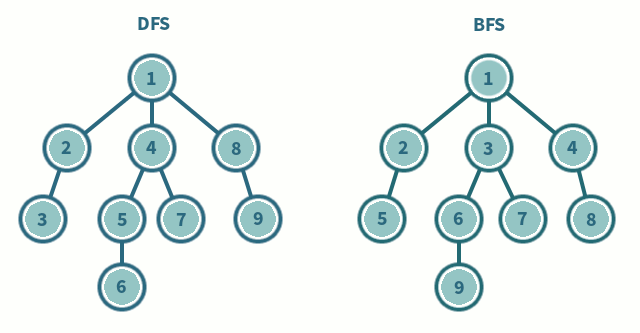
출처: 나무 위키 - 너비 우선 탐색
자주 등장하는 유형
BFS, DFS 를 활용할 수 있는 문제는 꽤 많다. 주로 2차원 배열을 주고 어떠한 규칙을 가지고서 출발점부터 도착지점까지 탐색하는 유형이 많다.
예를 하나 들자면, 아래와 같은 2차원 배열이 있고 순번이 있다. 가령, 1번부터 12번까지 가는데 최단 거리를 묻는다던가, 도착 여부를 묻는다던가 하는식이다. 이동 방식 규칙도 주어지고 갈 수 있는 곳과 없는 곳 등 다양한 조건들이 주어진다.
[ 1 ][ 2 ][ 3 ]
[ 4 ][ 5 ][ 6 ]
[ 7 ][ 8 ][ 9 ]
[ 10 ][ 11 ][ 12 ]
// ex. 1은 이동 가능, 0은 이동불가다. 상,하,좌,우로만 1칸씩 이동 가능할 때 도착할 수 있는가?
// ex. 1은 이동 가능, 0은 이동불가다. 상,하,좌,우,대각선로 1칸씩 이동 가능할 때 최단 거리는?
[ 1 ][ 0 ][ 0 ]
[ 1 ][ 1 ][ 1 ]
[ 1 ][ 1 ][ 1 ]
[ 0 ][ 0 ][ 0 ]
BFS, 어떻게 구현하는데?
Java uses Queue!
위와 같은 탐색을 하기 위해선 선입 선출 구조의 Queue 를 사용하여 구현한다.
아래 그림과 같은 구조를 가졌으며, 인접한 노드를 우선적으로 탐색하는 방법을 구현 가능하다.

출처: 나무 위키 - 큐(자료구조)
선입선출의 구조로 이루어져 있기 때문에 인접한 노드를 우선적으로 탐색하는 것이 가능하다. 위의 그림을 예시로 들자면 1번 노드에서 갈 수 있는 곳은 2, 3, 4번 노드다. 출발 노드를 1번 노드라고 했을 때 1번 노드를 Queue 에 넣고 반복문을 실행한다.
Queue.add(1); // 1. 탐색을 시작할 1번 노드를 추가한다.
while (!Queue.isEmpty()) { // 2. 큐가 비어있지 않다면 반복문을 실행한다.
Node node = Queue.poll(); // 3. Queue 에서 노드를 꺼낸다. (1번 노드)
... // 4. (1번 노드와) 인접한 노드인 2, 3, 4번 노드를 Queue 에 추가한다.
}
Queue 에서 1번 노드를 꺼내 인접한 노드인 2, 3, 4 번 노드를 Queue 에 추가하고 이후
2번을 꺼내 인접한 노드를 추가하는 방식으로 구현할 수 있다. 이후 2번과 인접한 노드인 1번과 5번을 추가하게 되는데 선입선출 구조이기 때문에 뒷 순서로 배치가 된다.
Node node = Queue.poll(); // 2번 노드를 꺼내고 인접한 노드를 Queue에 추가한다.
// 꺼낸 노드: 1, 2
// Queue 상황
-------------------------
< < 3, 4, 1, 5 < <
-------------------------
// 1. 선입선출 구조이기 때문에 2번과 인접한 노드는 후순위로 배치되고,
// 2. Queue 에서 다음 값을 꺼낼 때 3번 노드가 나오게 된다.
// 3. 마찬가지로 3번와 인접한 노드를 추가할 때 해당 노드들은 후순위로 배치된다.
예시 문제
예제 링크 - Programmers1844
문제 설명
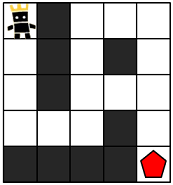 1.
1. 왕관을 쓴 캐릭터가 도착 지점인 빨간색 오각형 까지 도착해야 한다. 도착할 수 있는 경우의 수 중 최단 거리를 찾으면 된다. 도착할 수 없다면 -1 을 리턴한다. 시작점은 항상 [0][0] 이고 도착지점은 2차원 배열의 마지막 인덱스다.
 2. 주어진 2차원 배열은
2. 주어진 2차원 배열은 0과 1로 이루어져 있는데, 0 은 갈 수 없는 곳, 1 은 갈 수 있는 곳을 뜻한다.
 3.
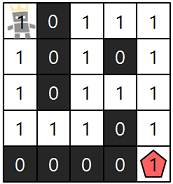
3. 왕관을 쓴 캐릭터가 빨간색 오각형 까지 도착하는 최단 경로를 찾으면 아래와 같다. (최단거리는 11칸)
4. 도착이 가능하다면 최단 경로 를, 도착이 불가하다면 -1 을 return 하면 된다.
BFS 를 위한 준비물들
BFS 구현을 위해 조건에 맞는 준비물들이 필요하다. 대표적으로 4가지 준비물이 필요하다.
탐색 방향의 조건, 상, 하, 좌, 우만 가능한가? 아니면 대각선도 가능한가?갈 수 있는 곳과없는 곳의 조건- 탐색한 곳은
재탐색하지 않아야한다. 도착 가능의 여부인가?최단 거리인가?
1. 탐색 방향의 조건
탐색 방향의 조건 이동이 가능한 방향, 거리를 뜻한다. 체스, 장기 말들이 2차원 배열에서 움직인다고 생각하면 이해가 쉽다. 문제마다 다르겠지만 보통은 현재 위치에서 1칸씩만 이동이 가능하며 상,하,좌,우,각각의 대각선 방향이 전부이다. 3차원으로 넘어가면 Z 축까지 포함시켜서 탐색을 할 수 있다. 예시의 문제에서는 상, 하, 좌, 우만 가능하며 대각선 방향으로는 불가하다.
코드로 풀어낸다면 2차원 배열에서의 상, 하, 좌, 우의 위치는 다음과 같다.
int[][] map = new int[10][10]; // 10x10 2차원 배열
// 상,하,좌,우
상: map[-1][0]; // 기존 위치에서 {-1, 0}
하: map[+1][0]; // 기존 위치에서 {+1, 0}
좌: map[0][-1]; // 기존 위치에서 {0, -1}
우: map[0][+1]; // 기존 위치에서 {0, +1}
기존 위치에서 [-1][0],[+1][0],[0][-1],[0][+1] 의 위치로 움직이면 상, 하, 좌, 우 위치가 된다. 여기서 배열의 크기를 벗어나는 인덱스를 주의해야 한다. 대각선의 방향은 [row][column] 모두 +1이 되거나 -1이 되는 경우의 수가 되겠다.
탐색 방향의 조건인 상, 하, 좌, 우는 아래와 같이 구현할 수 있다.
중요한 것은 기존 위치에서 row 혹은 column 중 하나만 ±1 을 하는 것이다
private static final int[] ROW = {1, -1, 0, 0};
private static final int[] COLUMN = {0, 0, 1, -1};
for (int i = 0; i < 4; i++) {
int newRowIndex = rowIndex + ROW[i];
int newColumnIndex = columnIndex + COLUMN[i];
map[newRowIndex][newColumnIndex] // 상, 하, 좌, 우
}
위의 코드로 탐색의 조건인 상,하,좌,우를 구현했다면 아래의 코드로 2차원 배열의 범위를 체크해준다. 음수 인덱스는 없으므로 0보다 커야 하고, 주어진 배열의 사이즈보다 큰 인덱스는 존재하지 않으므로 작은지 체크해주는 조건문을 구현해야 한다.
if (newRowIndex >= 0 && newRowIndex < mapSize
&& newColumnIndex >= 0 && newColumnIndex < mapSize) {
// ...
}
위의 두 코드를 합치면 아래처럼 작성할 수 있다.
private static final int[] ROW = {1, -1, 0, 0};
private static final int[] COLUMN = {0, 0, 1, -1};
for (int i = 0; i < 4; i++) {
int newRowIndex = rowIndex + ROW[i];
int newColumnIndex = columnIndex + COLUMN[i];
if (newRowIndex >= 0 && newRowIndex < rowSize
&& newColumnIndex >= 0 && newColumnIndex < columnSize) {
// TODO: logic...
}
}
이렇게 새로 만들어진 [newRowIndex][newColumnIndex] 를 통해서 탐색을 시작할 수 있다.
2. 갈 수 있는 곳과 없는 곳의 조건
탐색 방향의 조건을 구현했으니 이제는 갈 수 있는 곳, 없는 곳을 구현할 차례다. 예시 문제에서는 갈 수 있는 곳을 1 로, 없는 곳을 0 으로 주었다. 이 조건을 토대로 조건문을 작성해주면 된다.
if (newRowIndex >= 0 && newRowIndex < rowSize
&& newColumnIndex >= 0 && newColumnIndex < columnSize
&& map[newRowIndex][newColumnIndex] == 1 // 갈 수 있는 곳이라면,
) {
// logic...
}
조건문에 한 줄 추가하면 된다. 주어진 문제에서 1은 갈 수 있는 곳이다. (아래에서 후술하겠지만 탐색 조건은 효율성, 조건에 따라 바뀐다.)
3. 탐색한 곳은 재탐색하지 않아야 한다.
탐색 했던 곳을 또 탐색하게 된다면 무한 루프에 빠지거나 시간 복잡도 효율이 크게 떨어진다. 이미 탐색한 곳을 제외하는 조건문을 추가하자. 주어지는 2차원 배열과 같은 크기의 2차원 배열을 boolean 타입으로 선언한다. 이후 탐색 여부를 확인해주는 조건문을 추가하자.
boolean[][] isVisited = new boolean[rowSize][columnSize];
if (newRowIndex >= 0 && newRowIndex < rowSize
&& newColumnIndex >= 0 && newColumnIndex < columnSize
&& map[newRowIndex][newColumnIndex] == 1
&& !isVisited[newRowIndex][newColumnIndex] // 방문하지 않았다면,
) {
// logic...
}
조건문을 시작하기 전, 후 등을 통해 isVisited[][] 배열을 true 로 바꿔주어야 한다.
boolean[][] isVisited = new boolean[rowSize][columnSize];
if (newRowIndex >= 0 && newRowIndex < rowSize
&& newColumnIndex >= 0 && newColumnIndex < columnSize
&& map[newRowIndex][newColumnIndex] == 1
&& !isVisited[newRowIndex][newColumnIndex] // 방문하지 않았다면,
) {
isVisited[newRowIndex][newColumnIndex] = true; // 방문 처리
}
4. 도착 가능의 여부 인가? 최단 거리인가?
4-1 도착 가능의 여부일 경우
도착 가능의 여부는 위의 isVisited[][] 배열을 통해 확인할 수 있다. 탐색 조건에 해당되는 즉시 방문 처리를 하기 때문에 도착 지점의 인덱스를 출력해보면 알 수 있다.
System.out.println(isVisited[rowIndex][columnIndex]);
boolean 기본 값이 false 이므로 정확한 디버깅이 필요하다.
4-2 최단 거리일 경우
최단 거리의 예시는 조금 다르다. 최단 거리를 어떻게 찾느냐에 따라 다르겠지만 해당 문제에서는 주어진 2차원 배열의 값을 변경하는 식으로 접근했다. 시간 복잡도 및 효율성을 위해 후술하겠다는 말을 기억하는가? //TODO 링크 달리나? 위의 4가지 준비물은 BFS 구현을 위한 기본적인 필수품(?)이고 응용을 해서 구현해보자.
예시 문제를 풀어보자
예제 링크 - Programmers1844
문제 설명은 생략하고 코드와 함께 설명한다.
import java.util.*;
class Solution {
/* 상,하,좌,우 탐색 조건 */
private static final int[] DX = {1, -1, 0, 0};
private static final int[] DY = {0, 0, 1, -1};
/* 재탐색 금지를 위한 조건문 */
private static boolean[][] isVisitedByBfs;
/* 주어진 2차원 배열의 최대 사이즈 */
private static int maxRowSize;
private static int maxColumnSize;
public int solution(int[][] maps) {
/* 주어지는 2차원 배열의 최대 사이즈로 할당한다. */
int answer = 0;
maxRowSize = maps.length;
maxColumnSize = maps[0].length;
/* 재탐색 금지 배열 초기화 */
isVisitedByBfs = new boolean[maxRowSize][maxColumnSize];
/* BFS 탐색 메서드 */
bfs(maps);
/*
도착지점이 0 이면 -1을, 아니라면 maps의 값을 리턴한다.
이렇게 하는 이유는 bfs(); 메서드를 보면 알 수 있다.
*/
return maps[maxRowSize - 1][maxColumnSize - 1] > 1 ? maps[maxRowSize - 1][maxColumnSize - 1] : -1;
}
private static void bfs(final int[][] maps) {
/*
Queue 자료구조를 선언한다.
int[] 로 선언하는 이유는 2차원 배열의 인덱스를 그대로 담기 위함이다.
탐색 시작 위치는 항상 0, 0 이다.
*/
final Queue<int[]> queue = new LinkedList<>();
final int[] startPosition = {0, 0};
queue.add(startPosition);
/* Queue 가 비어있을 때까지 반복문을 수행한다. */
while (!queue.isEmpty()) {
/*
queue 에서 값을 꺼낸다.
꺼낸 값에서 rowIndex 와 columnIndex 를
변수로 선언한다.
*/
final int[] position = queue.poll();
final int rowIndex = position[0];
final int columnIndex = position[1];
/* 해당 위치를 방문처리 한다. */
isVisitedByBfs[rowIndex][columnIndex] = true;
/* 상,하,좌,우 탐색을 시작할 반복문이다. */
for (int i = 0; i < DX.length; i++) {
/* 새로운 rowIndex와 columnIndex 를 선언한다. */
final int newRowIndex = DX[i] + rowIndex;
final int newColumnIndex = DY[i] + columnIndex;
/* 1. 새로운 위치가 주어진 2차원 배열에서 유효한 위치인가? */
if (newRowIndex >= 0 && newRowIndex < maxRowSize
&& newColumnIndex >= 0 && newColumnIndex < maxColumnSize
/* 2. 아직 방문한 곳이 아닌가? */
&& !isVisitedByBfs[newRowIndex][newColumnIndex]
/* 3. 갈 수 있는 곳인가? */
&& maps[newRowIndex][newColumnIndex] != 0) {
/* 2차원 배열을 기존 위치에서 +1 시켜준다. */
maps[newRowIndex][newColumnIndex] = maps[rowIndex][columnIndex] + 1;
/* queue 에 새로운 위치를 추가시켜준다. */
queue.add(new int[]{newRowIndex, newColumnIndex});
/* 방문 처리 해준다. */
isVisitedByBfs[newRowIndex][newColumnIndex] = true;
}
}
}
}
}
주어진 2차원 배열의 값을 갱신(+1)하는 이유
문제의 정답은 최단 거리를 리턴하는 것이다. 현재 위치에서 갈 수 있는 곳들은 현재 위치에서 1번 더 가는 것이다. 만약, 현재 위치를 5번만에 도착했다면 현재 위치에서 다음 위치는 6번만에 도착하는 것이다. 즉 다음 위치는 현재 위치 + 1 인 것이다. 이를 코드로 표현한 것이다.
/* 2차원 배열을 기존 위치에서 +1 시켜준다. */
maps[newRowIndex][newColumnIndex] = maps[rowIndex][columnIndex] + 1;
예시 문제의 2차원 배열을 본다면 다음과 같다. 출발해보자.
// 시작단계
[ 1 ][ 0 ][ 1 ][ 1 ][ 1 ]
[ 1 ][ 0 ][ 1 ][ 0 ][ 1 ]
[ 1 ][ 0 ][ 1 ][ 1 ][ 1 ]
[ 1 ][ 1 ][ 1 ][ 0 ][ 1 ]
[ 0 ][ 0 ][ 0 ][ 0 ][ 1 ]
[0][0] 위치에서 출발해서 갈 수 있는 곳은? ● 로 표시한 곳이다.
0은 못가니 아래 위치 1개 뿐이다. 그렇다면 해당 위치를 기존 위치에서 + 1 시켜주면 된다.
// 시작점에서 갈 수 있는 곳
[ 1 ][ 0 ][ 1 ][ 1 ][ 1 ]
[ ● ][ 0 ][ 1 ][ 0 ][ 1 ]
[ 1 ][ 0 ][ 1 ][ 1 ][ 1 ]
[ 1 ][ 1 ][ 1 ][ 0 ][ 1 ]
[ 0 ][ 0 ][ 0 ][ 0 ][ 1 ]
이렇게 다음 위치는 현재 위치 + 1 이라는 공식을 가지고 있다.
// 2번만에 갈 수 있는 곳
[ 1 ][ 0 ][ 1 ][ 1 ][ 1 ]
[ 2 ][ 0 ][ 1 ][ 0 ][ 1 ]
[ 1 ][ 0 ][ 1 ][ 1 ][ 1 ]
[ 1 ][ 1 ][ 1 ][ 0 ][ 1 ]
[ 0 ][ 0 ][ 0 ][ 0 ][ 1 ]
현재 위치 + 1 공식으로 2차원 배열이 어떻게 바뀌는 지 확인해보자. 시작점 이후 Queue 에서 1번 꺼냈을 때, 시작점의 인접한 모든 노드를 꺼냈을 때, 갈 수 있는 모든 곳 등
즉 2번만에 갈 수 있는 곳
// 2번만에 갈 수 있는 곳
[ 1 ][ 0 ][ 1 ][ 1 ][ 1 ]
[ 2 ][ 0 ][ 1 ][ 0 ][ 1 ]
[ 1 ][ 0 ][ 1 ][ 1 ][ 1 ]
[ 1 ][ 1 ][ 1 ][ 0 ][ 1 ]
[ 0 ][ 0 ][ 0 ][ 0 ][ 1 ]
인접한 노드들을 방문처리 하면서 현재 위치 + 1 로 갱신해준다.
// 3번만에 갈 수 있는 곳
[ 1 ][ 0 ][ 1 ][ 1 ][ 1 ]
[ 2 ][ 0 ][ 1 ][ 0 ][ 1 ]
[ 3 ][ 0 ][ 1 ][ 1 ][ 1 ]
[ 1 ][ 1 ][ 1 ][ 0 ][ 1 ]
[ 0 ][ 0 ][ 0 ][ 0 ][ 1 ]
// 8번만에 갈 수 있는 곳
[ 1 ][ 0 ][ 1 ][ 1 ][ 1 ]
[ 2 ][ 0 ][ 8 ][ 0 ][ 1 ]
[ 3 ][ 0 ][ 7 ][ 8 ][ 1 ]
[ 4 ][ 5 ][ 6 ][ 0 ][ 1 ]
[ 0 ][ 0 ][ 0 ][ 0 ][ 1 ]
// 9번만에 갈 수 있는 곳
[ 1 ][ 0 ][ 9 ][ 1 ][ 1 ]
[ 2 ][ 0 ][ 8 ][ 0 ][ 1 ]
[ 3 ][ 0 ][ 7 ][ 8 ][ 9 ]
[ 4 ][ 5 ][ 6 ][ 0 ][ 1 ]
[ 0 ][ 0 ][ 0 ][ 0 ][ 1 ]
마지막 도착 지점까지 도착한 상황에서 도착점의 최단 거리인 11을 얻을 수 있다.
// 최종 도착점까지 도착한 상황
[ 1 ][ 0 ][ 9 ][ 10 ][ 11 ]
[ 2 ][ 0 ][ 8 ][ 0 ][ 10 ]
[ 3 ][ 0 ][ 7 ][ 8 ][ 9 ]
[ 4 ][ 5 ][ 6 ][ 0 ][ 10 ]
[ 0 ][ 0 ][ 0 ][ 0 ][ 11 ]


Comments